(Tompkins’ Quotes Continue)
The idea was received by some with derision, by others with acrimonious opposition. One reviewer remarked that Smyth’s book contained “more extraordinary hallucinations than had appeared in any other three volumes published during the past or present century.” A friendly reviewer summed up reaction to the book saying “it evoked numerous illustrations of envy, hatred, malice, and much uncharitableness from vain, flippant, and unqualified writers, the author being scoffed at, traduced, worried and all but argued with, by opponents who only succeeded in proving their egotistic inefficiency to apprehend the truth.”
…To this day, the lampooning persists. One modern writer on pyramidology still refers to Smyth as the world’s “pyramidiot.”
(excerpts taken from pp. 89 through 94 of Thompkins’s book)
[David’s] note: William Flinders Petrie came to the conclusion that Taylor and Smyth’s theory about the 25 inch cubit was wrong after going to the Pyramid himself and taking measurements.)
“…Summing up the results of his measurements in a book entitled The Pyramids and Temples of Gizeh (which he was able to publish with a fortuitous grant of 100 pounds from the Royal Society in London), Petrie remarked that he had never suspected, 15 years earlier, when he had first read Smyth’s fascinating theory, that it would be he who “would reach the ugly little fact which killed the beautiful theory…” …with success and recognition, Petrie turned from the romantic exploits of discovery to the prosaic minutiae of scientific archeology.”
(From p.106 of Thompkins’s book)
…Ironically, the next great investigator to throw light on the question of the Pyramid was…an agnostic and a sober structural engineer from Leeds, in the north of England, David Davidson.… But the more he attacked the data, the more he was obliged to assimilate it.… In the end he was to produce an encyclopedic literature in support …that the Pyramid was “an expression of the Truth in structural form” and that it “establishes the Bible as the inspired work of God.”
…On the question of the length of the Pyramid’s base, Davidson was to vindicate Smyth, yet avoid harming Petrie. According to Davidson, not only was Petrie’s survey correct, so was Smyth’s theory that the Pyramid’s base incorporated the length of the solar year.
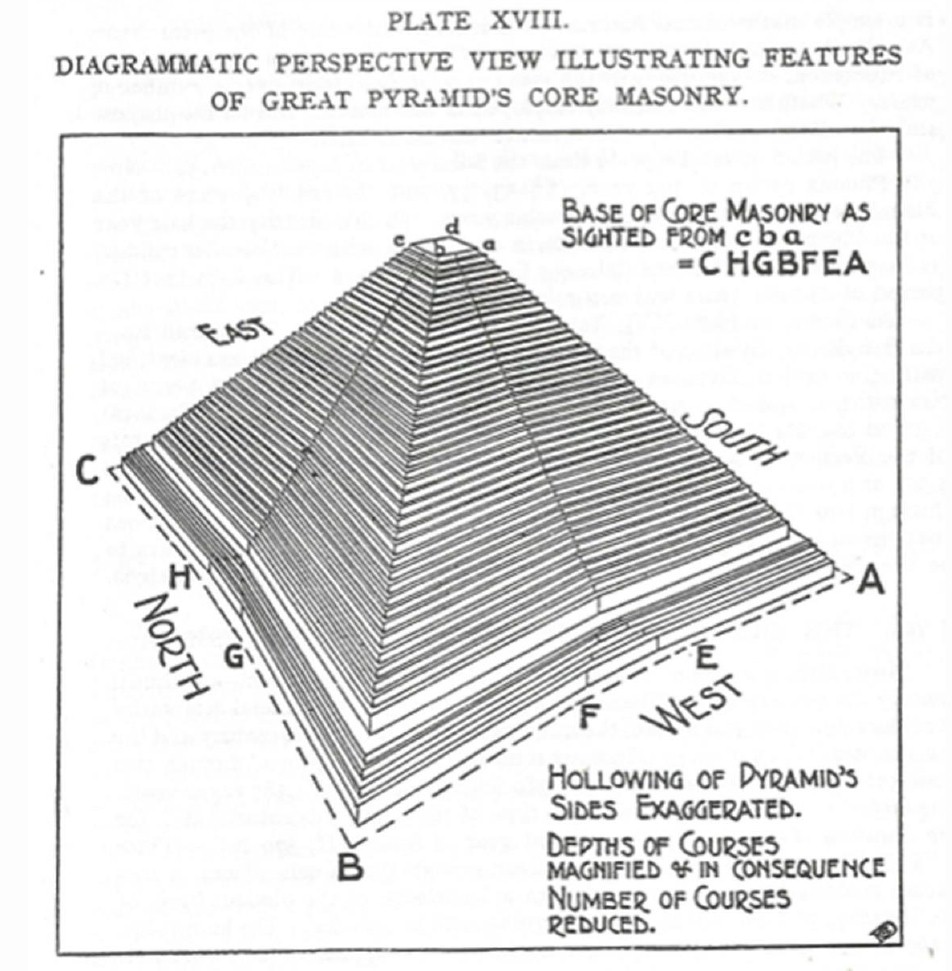
Petrie, with his meticulously careful measurements, had managed to observe a definite hollowing of the core masonry on each side of the Pyramid. The accuracy of this observation, normally invisible to the human eye, was revealed in Petrie’s lifetime in a dramatic aerial photograph taken accidentally at a specific time and angle by Brigadier P.R.C. Groves, the British prophet of air power. A similar line along the apothem, visible in an etching made by Napoleon’s savants, had been ignored for a century.
Davidson noted that Petrie had failed to extend this hollowing feature of the core material to his measurement of the outside casing. If this were done, a base length was obtained which fitted Smyth’s theoretical length to account for the solar year, to four points of decimal (page 108).
[Dan’s] note: Tompkins’ statement that “Petrie had failed to extend this holloing feature of the core material to his measurement of the outside casing,” is somewhat misleading. We will address this later.
…As Davidson put it: “By reason of this unfortunate omission, scientists have been led to believe that the theory of the late Astronomer Royal of Scotland—Professor Piazzi Smyth—requiring a Great Pyramid base circuit of 36,524 inches, was nothing more than a delusion.”
The ideal length postulated by Smyth for each side of the base in order to obtain the required length of 9131.5 Pyramid inches was 9141.1 British inches. Petrie’s figure, revised by Davidson, came out to 9141.4, or about a third of an inch too long.
[David’s] note: The Pyramid inch was thought by Smyth to be .001 of an inch longer than a regular British inch, thus 25 Pyramid inches were said to equal 25.025 British inches. Davidson’s calculations resulted in a British inch of 1.0011 of a Pyramid inch, resulting in a sacred cubit of 25.0275 inches. As noted in the main text, Davidson’s measurements would be within 1/3 of an inch over the entire length of one side of the base, of what today is the measurement needed to yield a sacred cubit, 10,000,00 of which equal the present estimate for the polar radius of the earth. Again only one of the sides was being carefully measured, apparently the north side.
According to Davidson, the hollowing effect would give three basic lengths of the year as recorded in the base of the Pyramid: an outer or shortest length, from corner to corner, bypassing the hollowing, a second, slightly longer, which included part of the indentation of the four hollowed faces at the base; and a third, which included the entire angle within each hollowed face.
These three measurements, which could have been performed by the ancients at their leisure, could have given the equivalents, according to Davidson, of the three lengths of the year as computed by modern science: the solar, the sidereal, and the anomalistic years, each of which is dependent on the system used for observation.
The academicians rebutted that all this was purely attributable to chance. An American naval officer who dabbled in digging at Giza remarked that “if a suitable unit of measurement is found— say versts, hands or cables—an exact equivalent to the distance of Timbuktu is certain to be found in the roof girder work of the Crystal Palace, or in the number of street lamps in Bond Street, or the specific Gravity of mud, or the mean weight of an adult goldfish.”
[David’s] note: A typical agnostic and atheistic insult in keeping with the mentality often exhibited by evolutionists.
(Dan’s] note: the problem with the derisive statement that “an exact equivalent to the distance of Timbuktu is certain to be found in the roof girder work of the Crystal Palace,” is that there is no relevant connection between the Great Pyramid’s construction to the Crystal Palace’s roof girder system. For while some multiple of the length of British measured “versts, hands, or cables…of the Crystal Palace” might be shown to equal the distance to Timbuktu, none of these nor “the number of street lamps in Bond Street, or the specific Gravity of mud, or the mean weight of an adult goldfish” prophetically anticipated, by a ratio of one such measure to one day (as did the biblical cubit), the three types of years that would result with the Amos eclipse of the 8th century BC (discussion following).
But Davidson’s conclusions were to reopen the entire subject of Pyramid measurements and breed a whole new school of pyramidologist.
The solar year is obtained by observing the exact time between two successive vernal or autumnal equinoxes, when the day is exactly as long as the night. It is now 365 days, 5 hours, 48 minutes and 49.7 seconds, or in decimals: 365.2422. The sidereal year (from the Latin sidus, for star) is the time it takes a star to reappear in the same spot in the sky, as seen by an earth observer.
It is about 20 minutes longer than the solar year, or 365.25636 days. This 20-minute lag causes what is known as the precession of the equinoxes, which comes 20 minutes earlier each year in relation
to the stars behind the equinoctial point. The anomalistic, or orbital, year is the time it takes the earth to return to the point in its elliptical orbit nearest the sun, or perihelion. This is about 4¾ minutes longer than the sidereal year. According to Davidson, not only does the Pyramid give this value, but it gives the number of solar years it takes for the perihelion to complete a full circle of 360º (p. 111).
[David’s] note: In all honesty, Taylor and Smyth suspected that each side of the Pyramid represented each day of a solar year as 25.025 inches. They struggled to verify this. It was David Davidson, who apparently became a Christian through his study of the Great Pyramid, who showed this.
[Dan’s] note: Davidson used Petrie’s calculations but not all his assumptions, and so came to different conclusions. The issue was where on the platform the Pyramid began. The platform is a flat and level surface on top of which the Great Pyramid sits. The platform is between 20” to 21” high and is made of carefully cut limestone
blocks. Beyond the platform is abutting pavement. Under the platform and pavement is more or less leveled ground. It was probably under the platform, not the pavement which abutted to the platform, under which the Pyramid’s sockets lay. Their exact relationship to the Pyramid was interpreted differently by Petrie and (later), Davidson, and has led to a long-standing debate. Petrie believed that the Pyramid’s slanted edges ‘continued’ through the platform and ended at the bottom of the sockets’ outer corners. (The sockets vary in depth [though in one case depth is barely apparent], though we don’t know why.) Davidson believed that the Pyramid’s slanted edges ended on the platform directly above the sockets’ outer corners. This means that Petrie conceived of the Pyramid’s corners, by which we mean where they were visible, as more inward than where Davidson supposed. Thus depending on which viewpoint one takes—Petrie’s or Davidson’s—the length of a base side and the base perimeter of the Great Pyramid differ. Davidson argued that the New Construction (i.e. Davidson’s construction) in comparison with Petrie’s Construction, was justified because the New Construction held up to critical analysis. By “critical” analysis Davidson meant a number of evidences, not all of which I accept (e.g. Davidson’s belief that the late Egyptian chronologies were all fictitious and designed so that the total number of years reigned by gods and kings amounted to the same number of pyramid inches in the Great Pyramid. Chapter 9 shows that Africanus’ version of Manetho’s chronology of Egyptian pharaohs, with certain reigns overlapping, is correct and therefore not fictitious.
However, Davidson did give at least one line of evidence which by itself is proof enough that the New Construction is the correct view. It is that three measurements based on the corners of the Great Pyramid demonstrate the three types of year: i.e., the solar, the sidereal, and the anomalistic years. The below illustrations show the different interpretations of Petrie and Davidson about where on the platform the Pyramid’s corners are visible. Note: what Thompkins calls “the platform” is termed “pavement” in Davidson’s Plates XXI and XXII.
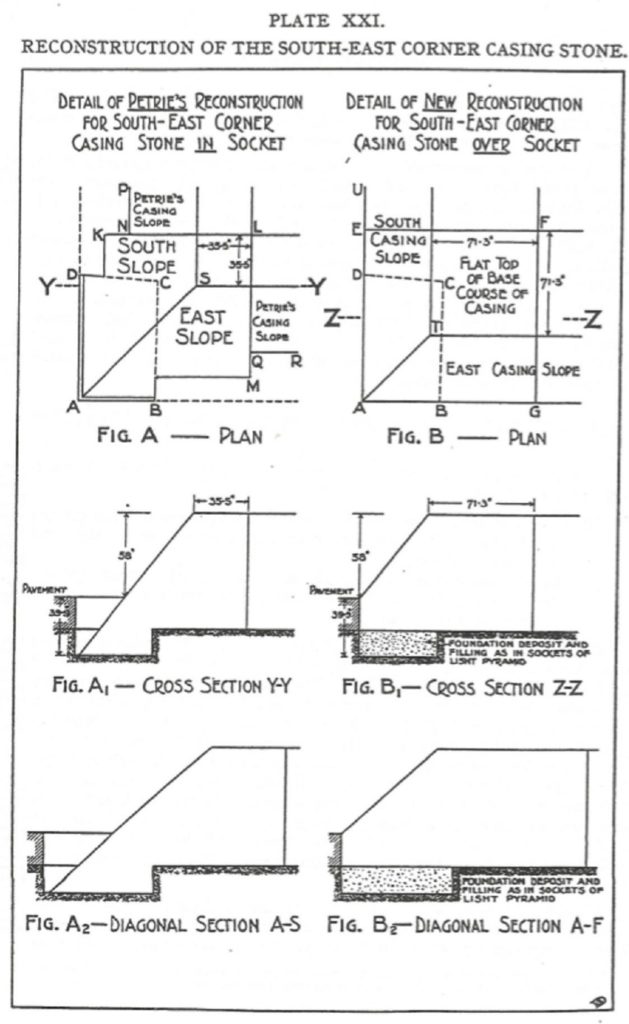

Of the two illustrations, I personai!J find Plate XXI the clearest explanation of where the Pyramid’s corner meets the pavement (i.e.,platform), especiai!J in Figures A1,B 1,A2, and B2. Recall that the Petrie/ Davidson debate (so to speak) has been longstanding between suppotters on both sides. Petrie’s view is often taken up qy skeptics who need a lesser number of Pyramid inches to show that no Divine plan was handed down to human agency for the Pyramid’s design. On the other hand, Davidson’s supporters point out that only a Divinely given plan could explain the three perimeter measurements which represent the three types of years—the solar, the sidereal, and the anomalistic. This is shown in the next two illustrations below: In Plate XVII is shown the Base of Core Masonry. This is the plainer stones tourists see when they go visit the Great Pyramid. But originally the Great Pyramid had an outer limestone casing. (Almost all of the finished casing was removed centuries ago to construct other buildings, such as Mosques.) And so, the debate is whether or not the limestone casing followed the hollowing-in effect (Davidson’s view), or whether the limestone ‘erased’ the underneath ‘crease’ so that the sides were perfectly smooth (Petrie’s view). In favor of Petrie’s view is that Menkaure’s pyramid, the smallest of the three major pyramids and only one of three Egyptian pyramids (of 80) to have the center ‘crease’, has been discovered by pyramidologists Maragioglio and Rinaldi to have granite casing which ‘erased’ the crease by forming a flat surface. Therefore it would seem the Great Pyramid would likewise have had a casing which formed a flat surface. If so, then Davidson’s measurements for at least the sidereal and anomalistic years are not represented in the Great Pyramid. We will come back to this point a little later.
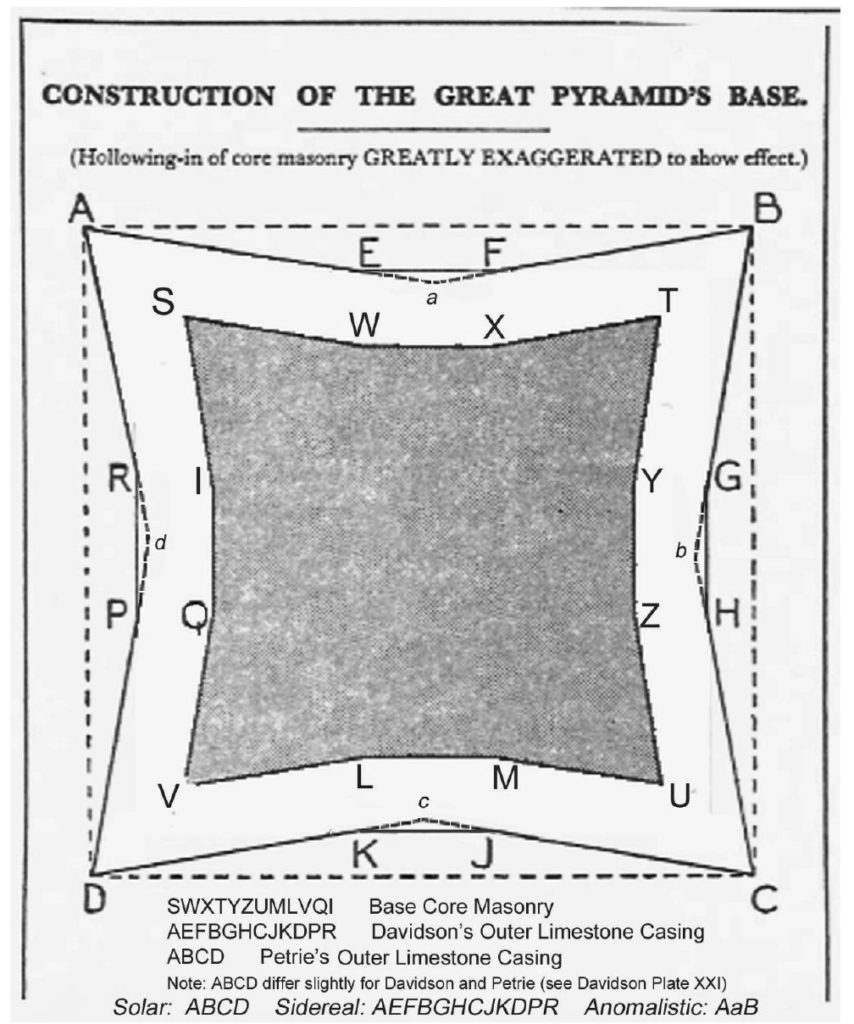
The above illustration shows Petrie’s and Davidson’s proposals for the outer limestone casing. Petrie’s is ABCD. Davidsons’s is AEFBGHCJKDPR. Davidson explains that Petrie failed to carry out the hollowing-in of the cored masonry to the outer limestone casing. That is, Petrie pushed the limestone casing all the way to ABCD instead of allowing the limestone casing to ‘mirror’ the base core masonry by paralleling the various angles of it. The results for Petrie were measurements that had no particular significance or reference beyond the Pyramid itself. Thus he dismissed the work of such men as John Taylor and Piazzi Smyth, who had attempted to show that the basic unit of measurement in the construction of the Great Pyramid was a sacred cubit of 25 pyramid inches (Smyth’s value for a pyramid inch was 1.001 B.” [i.e. British inches]) Petrie, who as a younger person was drawn to Smyth’s idea of a Divine plan behind the Pyramid’s construction, now believed his surveys proved Smyth wrong. Petrie said he never imagined it would be he who would “kill the beautiful dream” [of Smyth]. He also stated:
“there is no authentic example, that will bear examination, of the use or existence of any such measure as a ‘Pyramid inch,’ or of a cubit of 25.025 British inches.”
[Note: Smyth’s figure of 1/10,000,000th polar radius of the earth was 25.025 B.” (i.e., 25 x 1.001 B.”), based on what his contemporaries believed was the distance of the polar radius of the earth. He believed this length was that of the sacred (biblical) cubit.]